A Questionable Method of Winning Using Constant Betting and Doubling in a Virtual Racecourse
PDFダウンロード(36 pages. Download) Published online:12 Aug, 2025
xlsm files
You can download Microsoft Excel file with macro, using in this paper.
Virtual horse racing data 223MB
Standard model of this paper for 10,000 races 22MB
Standard model of this paper for 100,000 races 32MB
Abstract
In this paper, I propose improvements to a dubious method of winning in horse racing using the strategies of constant betting and doubling (the Martingale method of progressive betting) such that rewards can be obtained with lower risk. Since it is said that applying doubling generally leads to bankruptcy, I introduce an modified method such that the risk is reduced. That is, we use doubling as a last resort when the uncollected amount reaches a predetermined value. Before using the doubling method, we start by placing a place ticket bet on the first-ranked horse with the lowest odds whose hit rate is the highest. After a win, we skip all subsequent races to avoid risking a loss. While the uncollected amount remains under a predetermined value, we continue placing win ticket bets on the first-ranked horse with odds sufficient to clear the uncollected amount. After the uncollected amount reaches the predetermined value, we use doubling for the first-ranked horse and constant betting for the second-ranked horse. By this method, we can keep the risk within a tolerable level. To analyze this strategy, I experimented by entering competitions in a virtual racecourse. While the stochastic data such as hit rate are different from actual real-world data, this model shows an upward trend with small valleys (the risk). While it is still necessary to consider what would happen in actual operation, I believe that this study can become a foothold to develop a winning method in the future.
Keywords: Doubling. Martingale. Horse racing. Constant betting. Virtual racecourse.
1 Introduction
In this paper, I consider the use of doubling to be a last resort as a method of winning. Doubling is well known as a questionable winning method. Turner (1998) compares doubling to constant betting by using computer simulations. Many websites and videos, such as Umameshi.com (2021), introduce its application to horse racing.
In Ohyama (2025), I proposed some methods to apply doubling to horse racing. In the paper, the input amount (wager) is set to the uncollected amount divided by a predetermined value. Furthermore, some additional strategies are proposed: (1) Start betting on the first-ranked horse with low odds whose hit rates are highest. (2) Skip all subsequent races after clearing the uncollected amount (the temporary accumulated loss). (3) Increase the coefficient when the uncollected amount becomes large. By these strategies, we can reduce the risk to some extent. However, a simulation consisting of 10,000 races finds that there is a risk that the amount of a single bet could rise to as much as 100,000 yen.
This paper is a continuation of the work presented in Ohyama (2025). First, I prepare the simulation data (data generated through simulated races in a virtual racecourse), including both win and place tickets. In Japan, place tickets are a type of bet where rewards are obtained when the betting horse comes in first, second, or third place (or first or second place when the number of horses is less than 8). While the returns (winnings) are lower, the hit rate (chance of winning) is higher. Considering an investment where making a profit is a priority, the high hit rate is a big attraction, even if it is a small amount.
Further, I consider to how to use constant betting to our advantage. Given a certain degree of values for hit rate and recovery rate, there is no risk of incurring a large loss with constant betting. Therefore, until and unless a certain amount of loss occurs, it is more effective to continue using constant betting (compared to the riskier doubling method) and wait for profits to emerge. Additionally, in horse racing, we can purchase multiple tickets. While using the risky doubling method with one ticket type, we can simultaneously employ constant betting with another ticket type. This may help to reduce the risk.
By making effective use of the advantages and trade-offs of doubling and constant betting, I consider whether there is an optimal winning method with less risk.
In Section 2, I explain the process of constructing the simulation data used in subsequent sections. Apart from the data, Section 2 is not related to the methods discussed in those sections and can be skipped if there is no interest in the data creation process.
Section 3 is the core of this paper. In Section 3.1, I define constants and variables, and I formulate the standard model. In Section 3.2, I show an example. In Section 3.3, I show the results of 100,000 races using the parameters and models of section 3. Looking ahead to actual operation and practical use, I confirm whether there are any bad cases or outcomes in the 100,000 simulated races.
Finally, in Section 4, I conclude this paper.
I believe successful methods of winning do exist. I hope that this study may offer support to develop them.
2 Constructing horse racing data
See page 4 of the pdf file.
3. A method of combining constant betting and doubling
3.1. Steps of the model
See page 20 of the pdf file.
3.2 An example of the model
I will show one example using data0 from Section 2. Table 11 shows the configuration of the parameters.
Table 11. An example of parameters
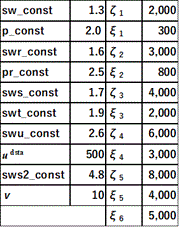
When written in descriptive sentences, it looks like this:
(i) We skip all races until the first-ranked horse’s odds are 2.0 or less.
(ii) If the odds are 1.3 or lower, then purchase a 100-yen win ticket for the first-ranked horse. If the odds are between 1.4 to 2.0, then purchase a 100-yen place ticket for the first-ranked horse.
(iii) If the horse bet on in (ii) won, then skip all further races for that day. If that horse lost, bet on the first-ranked horse whose odds are between 2.0 to 2.6 such that the loss is eliminated by a win.
(iv) Similarly, if there is an uncollected amount (temporary loss) of 200 yen after the race, then bet on the first-ranked horse whose odds are between 3.0 to 3.6 such that the loss is eliminated by a win.
(v) If there is an uncollected amount of 300 to 500 yen after the race, then purchase 100-yen tickets for the first- and second-ranked horses. (This is done not to eliminate the losses all at once, but in the hope that it will reduce them, even if only a little.)
(vi) If there is an uncollected amount of over 500 yen after the race, then bet using doubling for the first-ranked horse and purchase a 100-yen ticket for the second-ranked horse.
Table 12 shows the results of the first 16 races where bets were placed. (Races in which we don’t place bets are not displayed.) We can see that we start betting with races where the odds are low, so there may be an interval of waiting before betting. After a win, all remaining races are skipped, which reduces the number of races significantly.
Table 12. First 16 betting races
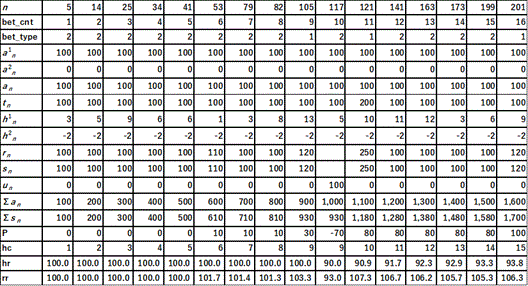
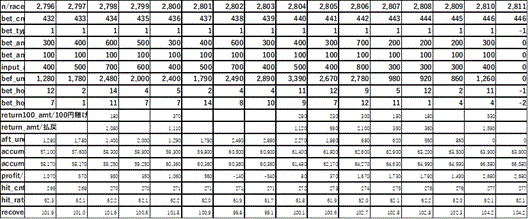
Fig. 1 and Table 13 show the results of 10,000 races. Fig. 1(a) shows the profit change throughout the 10,000 races. We can see a gradual upward trend. There are small, short valleys, but the deep valleys that existed in Ohyama (2025) are gone. Fig. 1(b) shows the first 500 races and Fig. 1(c) shows the first 2,000 races. In Fig. 1(b), the input amount for the first-ranked horse reaches 300 yen at the 496th race. However, this amount is nothing to be afraid of. Similarly, at the 1,155th race, we must spend 600 yen to bet on the first-ranked horse. Still, this amount is not a psychological burden. Fig. 1(d) shows the worst case. At the 2,806th race, we must spend 700 yen for the first-ranked horse, and 100 yen for the second-ranked horse, for a total of 800 yen. This is the biggest crisis point in the 10,000 races, 1,522 of which contain bets (the betting count).
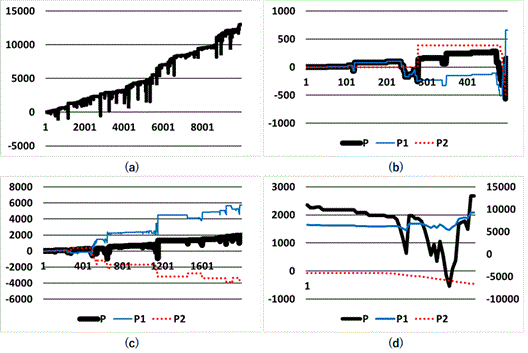
Fig. 1. An example of the combination model. (a) Results of 10,000 races. (b) First 500 races. (c) First 2,000 races. (d) The worst cases (races 2,757 to 2,811).
The first thing to note is that approximately 8,500 out of 10,000 races are skipped. As Cardano says, the best bet is not to gamble at all. The first time we bet, we bet on a horse with odds of 2 or lower, so our chances of winning are high. Moreover, by making a place bet, our chances of winning are increased even further. Even if the bet loses, we follow that loss with a bet on the most popular horse whose odds are between 2 and 2.6, which gives us a relatively high chance of winning. Similarly, even if there is a second loss, we follow that with a bet on the most popular horse whose odds are between 3 and 3.6. Although the odds are more than three times as high, the bet-on horse is still the most popular, and its chances of winning are high. If there is a third loss, we will be betting on the most popular and the second most popular horses at the same time. At this last step, doubling will be applied to the most popular horse. Further, when doubling is applied, the coefficient b is set in a stepped manner so that input amount does not become large. (See Section 6 of Ohyama 2025)
Table 13. Detail of the worst cases
The current parameter settings were decided after hundreds of trial-and-error attempts. I believe that this is near optimal for data0, but I don't know if it is the best configuration in general. I also don't know if these parameters will work well with examples other than data0 until they are actually tested. However, in the worst case scenario with data0, we only needed to bet 800 yen. Even if only small changes were made to the data, it is reasonable to expect that there would not be any major losses. To follow up, I decided to check the results using the simulation data for 100,000 races.
3.3. Results of 100,000 races
Table 14 and Fig. 2 show the results of 100,000 races. Surprisingly, the maximum input amount was found to be 800 yen for all 10 datasets. As Fig. 2 shows, all the examples show a smooth upward trend.
The standard model implemented this strategy: (I) Start betting in races with a high probability of winning. (II) Try to avoid betting in too many races. (III) When the uncollected amount is large, bet on the second most popular horse, in addition to the most popular horse. (IV) Apply doubling to the most popular horse when the uncollected amount increases further. I believe that these efforts are the reason for the good results.
Table 14. Results of 100,000 races
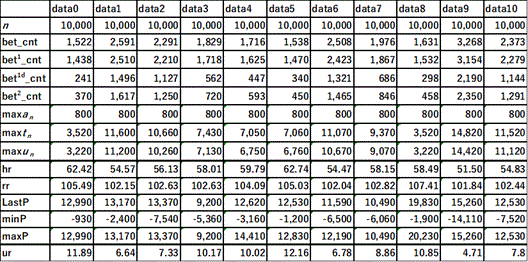
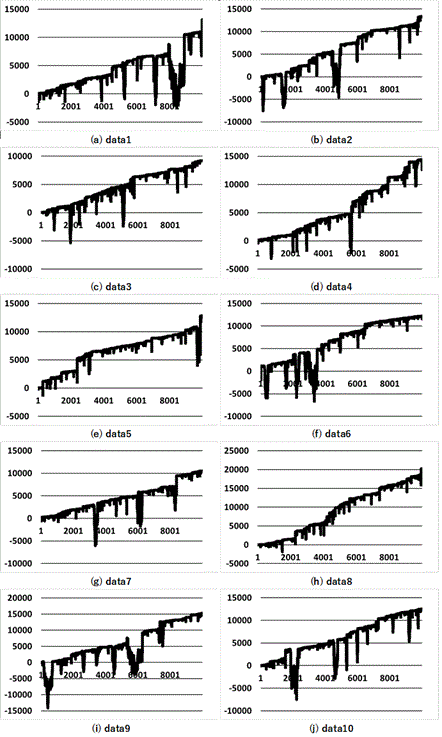
Fig. 2. Results of 100,000 races.
4 Conclusion
In this paper, I proposed a modified version of the doubling method in order to make a profit with low risk in a virtual racecourse. In this model, rather than using predictions, we continue to bet on the first-ranked or the second-ranked horse.
The procedure is relatively simple, as shown in Section 3.1.
Using doubling for the first-ranked horse has the power to reduce losses to zero all at once while the risk stays high. Using constant betting for the second-ranked horse also has the power to reduce large losses while the hit rate stays low. However, the sum of the hit rates of the first- and second-ranked horses is over 50%. Rather than implementing a method that relies solely on doubling for just one horse, hopefully this offers a way to offset losses with low risk.
I designed the model and adjusted the parameters by using data gathered from 10,000 races. I confirmed the amount of risk present in the data through 100,000 additional races (10,000×10), with the goal of looking forward to practical use of the model in future races. In all 10 cases of 10,000 races each, we observed upward trends with a recovery rate of over 102%, despite temporary losses of 10,000 yen. Although the recovery rates are small, I believe that the presence of only small temporary losses is a great achievement. Considering the models of Ohyama (2025), the loss (maximum input amount) observed there was not stable. That is, we couldn’t determine the financial budget needed to prepare for actual operation. By contrast, with the model proposed in this paper, the balance drops by only about 10,000 yen at its deepest point. If the program is bug-free, and if the racing data and assumptions are correct, we can probably operate it safely with a capital between approximately 20,000 and 100,000 yen, but there is no guarantee that this range is valid.
Admittedly, this paper relies on a not-insignificant problem with the data that was used. Differences were found between the simulated data and actual racing data in terms of hit rates, recovery rates, and average returns.
Generating highly accurate data is not easy. It is difficult to provide a logical justification for the model. Many readers will be interested to see examples of practical applications. While the risk has been significantly reduced compared to that of the previous paper, it is still important to study this further. I would also like to try putting this model into practice.
From an investment perspective, the payback rate is important. However, care must be taken when inferring anything about recovery rates. Although the recovery rate in this paper was determined to be 102% for 100,000 races, this does not mean that 1 million yen can be turned into 1.02 million yen. Fig. 1(a) and data0 of Table 14 show examples of results where the recovery rate is 105%. However, the total input was 236,400 yen, and the total return was 249,390 yen. The total profit is less than 15,000 yen. At this stage, I'm not sure what to do to make even as much as 50,000 yen. Can this be achieved by increasing the initial investment amount? I would like to continue researching this question in the future. Further, of personal interest to those of us in Japan, when we make a profit of more than 500,000 yen in one year, we are taxed on that amount. Naturally, I would like to consider how to design a model to earn 500,000 yen in one year.
In Japan, the hit and recovery rates for each rank and horse number are published for each racecourse. By using these values, we can form a mental image of the occurrence of some event. For example, if the data show that the hit rate of the most popular horse is 33%, and that of the second is 20%, then we can imagine the probability of winning with the most popular horse as roughly the same as the probability of rolling a 1 or 2 with a die. Similarly, we can imagine the probability of winning with the first or second most popular horse is larger than the probability of getting heads on a coin toss. The probabilities of dice, coin tosses, and roulette wheels are easy to imagine and have been studied in depth. There are countless models, simulations, and computer games that use these tools. These concepts will also contribute to future research on the topic of horse racing.
When I started studying horse racing in 2021, I was mostly paying attention to doubling. I believed at the time that doubling was the strongest method, although proper configuration of the parameters was difficult. When I tried this strategy out in actual races, I suffered losses of over 200,000 yen, three separate times. Based on data from about 300 races, I realized that it would be dangerous to put this method into practice. I realized the importance of testing with simulation data from over 10,000 races. (Of course, how much data is actually needed is unclear.) I analyzed this topic intensively to write the previous paper, Ohyama (2025). Even though the model was showing an overall upward trend, I found that there were several instances of large losses that occurred during the 10,000 races. In horse racing, it is inevitable that a long losing streak will occur. Similarly, with simple doubling, it is inevitable that large losses will occur.
In this paper, I focused on constant betting as well as doubling. When applying constant betting, even with consecutive losses, the overall loss is small. I believe constant betting is a good method when starting to gamble. Doubling will naturally be considered when losses continue. Further, we can reduce risk by betting on different horses.
Betting on multiple horses can be considered as a type of portfolio, a concept which has been studied deeply in the field of investment. There is also room for further development of a betting portfolio using the method presented in this paper.
I did not submit this paper to a peer-reviewed journal. I would like to make my own methods public for now, without being influenced by extraneous opinions. As the author of this paper, I myself have doubts about using virtual race data. Regardless of the assumptions and accuracy of the data, I don't think the results are bad. However, I want to avoid being labeled a scammer by announcing this method without verifying its safety. I don't know whether this is really possible, but I intend to attempt it going forward. The results of the implementation will be published on my website at nirarebakun.com. If this turns out to be a success, the story may become famous naturally. Modifications to the model will also likely occur during its implementation. Once I have compiled these findings, I intend to write a peer-reviewed paper or book on this topic.
I think horse racing has two properties that make it stand out. One property is that, in some countries, the hit rates and recovery rates for each racecourse are made public. Alternatively, these values can be figured out through the patient collection of data. Another property is that our individual bets do not lower the odds, assuming that we do not bet very large amounts. This is a characteristic of gambling that perhaps didn't exist in Cardano's time. I am sure that more study will lead to further developments.
This man Cardano, whom I respect as a god, predicted his own death and left behind some famous quotes about gambling. In retrospect, this may not have been beneficial in terms of world peace. Many tragic incidents have occurred as a result of gambling. These cases seem to support his famous saying that gambling is not profitable. To date, mathematical and economic research on this topic has not been carried out in depth. This can be viewed as a bleak history marked by an utter failure to understand gambling, even though much time has passed. By contrast, high probability investment techniques are well studied despite the fact that there are no guarantees that profits will be made. When it comes to horse racing, the courts have proven that surefire ways of making profits in the hundreds of millions do exist.
It's difficult to predict how the world will change after high-probability methods of winning are developed, but I would like to imagine a bright future. It is said that the amount of money needed for retirement in Japan is 20 million yen. Many people are anxious about the future. Personal savings plans are taking priority, and the economy is worsening. Prices are rising, and the gap between rich and poor is widening. Many people think that being employed or working doesn't make their lives easier. I believe that if a successful method of winning can be developed, it will be possible to live a long, wealthy life and be happy with even a small amount of savings. (Still, I certainly don't want to see a world where young people reject work and attempt to live off gambling.) Personal savings will become less of a priority and economic activity will increase. I think it will give us more peace of mind. People cannot choose their parents or the country they are born into. I hope that it will be easier for people born into poverty to become wealthy. If that could happen, perhaps the world would be a little more peaceful.
Indeed, I continue to buy horse racing tickets and bet on the weekends. My current betting method differs from the model I wrote about here. Losing is far more common than winning. There is a Japanese term for horse racing called “Kanpai.” This means that if the officials determine that the start was not normal, the start will be restarted. However, this word reminds me of two other meanings. The second meaning is “to toast” and the third is total defeat. There is a song called the Toast Song in Verdi's opera La Traviata. I love this upbeat song and often play it on trumpet and sing it. But, whenever I lose at horse racing, a minor version of this opera plays in my head. My hope is that one day this paper will be accepted, and then I will be able to perform the toast as cheerfully as Luciano Pavarotti. “Libiamo!”
References
Box G. EP, Muller M. E. (1958). A note on the generation of random normal deviates. Ann. Math. Stat., 29, 610?611.
Ohyama T., (Published online 2025). Some Challenges for the Improvement of Doubling at a Virtual Racecourse.
http://nirarebakun.com/hr/hrpaper.html
Turner N. E., (1998). Doubling vs. Constant Bets as Strategies for Gambling, J. of Gambling Studies, 14, 413?429.
Umameshi.com, (Last update 2021).
https://www.umameshi.com/info/002.html [In Japanese]
競馬の研究?にはお金がかかります。寄付歓迎しております。
Horse racing research is expensive. Donations are welcome.

・なにかありましたらメールください。どうぞよろしくお願いいたします。

ご意見、ご感想、お問い合わせ、お願い等がございましたら、お気軽に、
 メール送信フォームからメールを送るか、
メール送信フォームからメールを送るか、
●掲示板に書き込むか、
どちらかお好きな方法で、ご連絡お願いいたします。
●大山崇のホームページの利用について
●大山崇のホームページ








 メール送信フォームからメールを送るか、
メール送信フォームからメールを送るか、