CW, LW and Karlsruhe are very heavy.
Manhattan-metric Voronoi diagram(Open 5/Sep/2000 : The 5th Revision Wednesday, 03-May-2006 23:25:49 JST)
Manhattan-metric Voronoi diagram is drawn by using distance function d(p,p(i))
d(p,p(i))=|x-x(i)|+|y-y(i)|
where (x,y) is the coordinate of p, (x(i),y(i)) is the coordinate of p(i), |a| is a sign of absolute value.
Special case
Manhattan Voronoi diagram for square lattice generators
Manhattan Voronoi diagram for radial generators 1
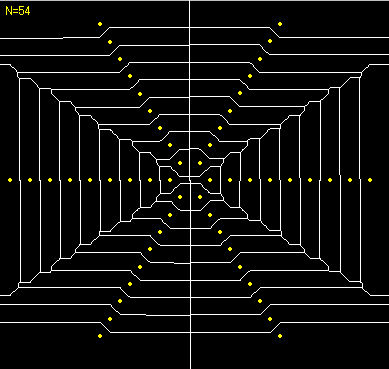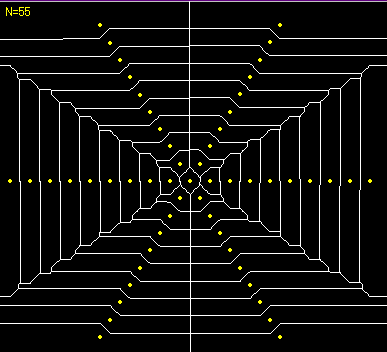Manhattan Voronoi diagram for radial generators 2
Manhattan Voronoi diagram for triangular lattice generators
Manhattan Voronoi diagram for hexagonal lattice generators
Algorithm
the concept is very close to that of the ordinary Voronoi diagram
Following algorithm is for the ordinary Voronoi diagram
i=1,...,N-1
j=i+1,...,N
Consider a bisector of p(i) and p(j)
k=1,...,N except for i and j
Consider a bisector of p(i) and p(k)
Calculate the points of intersection of bisector(i,j) and bisector(i,k)
next k
Add the points at x=0 and x=(the width of the screen) of the bisector of i and j into the points of intersections
Sort the points of intersections in terms of x coordinates
k=1,...,the number of intervals of the points of intersections
Let c be a midpoint of the interval of the points of intersection.
Let d be d(c,p(i))
h=1,...,N except for i and j
Let d' be d(c,p(h))
If d'<d then shout (Out!)
next h
If we did not shout, then draw the interval of the points of intersection
next k
next j
next i
but the bisector of Manhattan Voronoi diagram is not line.
it is conbination of horizontal half-line, diagonal line segment and horizontal half-line (type 1) or
vertical half-line, diagonal line segment and vertical half-line(type 2)
(See Okabe et al. Soatial tessellations 2nd ed. Fig. 3.7.2)
this conbination type is decided by the difference of x-coordinate and difference of y-coordinate.
that is, if difference of x-coordinates is larger than the difference of y-coordinates then type 2 and
if difference of y-coordinates is larger than the difference of x-coordinates then type 1
(I don't consider the case that the differences are exactly same because the probability is 0 since generators are made from random variables.)
By the way, I set y=400 x+? instead of the vertical half-line(x=?) of the type-2, sorry.
Java(man.java)
If you have a message, don't hesitate to send it by using
E-mail:
Easy subject (which starts with 'about nirarebakun.com') to understand, please.
Because I'm afraid to get a virus mail or ad-mail, I delete the mail if the subject is abnormal.
Good example for subject:
About nirarebakun.com:Voronoi diagram
About nirarebakun.com:I'm interested in Steiner problem
Bad example for subject:
'Hello', 'Thank you', 'How do you do', 'Please', 'I love you', 'Re', 'Document', 'Excel file', 'Product' and so on.
And don't attach the file when you send the first mail.
or
BBS
English Home of Takashi Ohyama
Japanese Home of Takashi Ohyama