2000 : The 13th Revision Thursday, 03-Jun-2010 22:12:51 JST)

Voronoi diagrams (Automatic version)	Ordinary	Multiplicatively Weighted /Area	Additively W /Area	PW(additively Weighted Power)	Compoundly W	LW(L_{weight} norm)
Higher-order	HMW	HAW	HPW	HCW	HLW
Elliptic	Manhattan	Supremum	Karlsruhe	Farthest-point
HElliptic	HManhattan Farthest-Point Manhattan	HSupremum	HKarlsruhe	Higher-order Farthest-point
line-segment	line-segments sometimes cross each other	line-segments need to cross each other	largest empty circle in a polygon
Higher order line-segment	Higher order line-segment (segnebts sometimes cross each other)	Higher order line-segment (segments need to cross each other)
Area of Voronoi Region /MW Area /AW Area	Delaunay Tessellation	order-2 Delaunay	Order-3 Delaunay	Farthest Delaunay
Delaunay some edges deleted	-	-	Extended Voronoi Edges	-	-
Voronoi area game for two	for three	for four	for five	for six	-
Voronoi diagrams (Click version)	Ordinary	-	Largest Empty circle in a polygon
Higher-order
-	Manhattan	Supremum	Karlsruhe	Farthest-point
HManhattan Farthest-Point Manhattan	HSupremum	HKarlsruhe
Area of Voronoi Region	Delaunay Tessellation	order-2 Delaunay	Order-3 Delaunay	Farthest Delaunay
Voronoi area game for two	for three	for four	for five	for six	-

Automatic version	Center problem	Empty circle, Largest empty circle	Largest empty ellipse
Click version	Center problem	Empty circle, Largest empty circle	-

There are some points (facilities) in a region. Let us assume that consumers use the nearest facility. Then, the Voronoi diagram explains the catchment area of each facility.
Let us define n points as p(1),...,p(n). The Voronoi region of p(i) is explained by
V(p(i)) = {x|d(x,p(i) ? [Note: Please check the change.] d(x,p(j), for all j(not i)}.
In the case of an Ordinary Voronoi diagram, the distance d is Euclidean.
The Voronoi diagram comprises the set of Voronoi regions,
{V(p(1),...,V(p(n))}.
An edge of an ordinary Voronoi diagram is generally a segment of a perpendicular at a midpoint.

Voronoi diagram for square lattice generators

Voronoi diagram like spider web 1

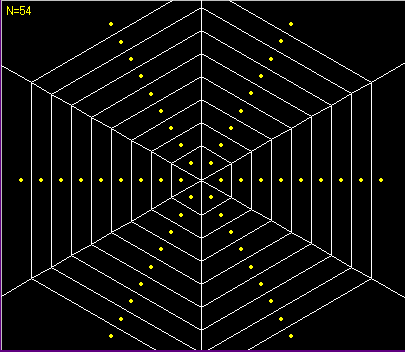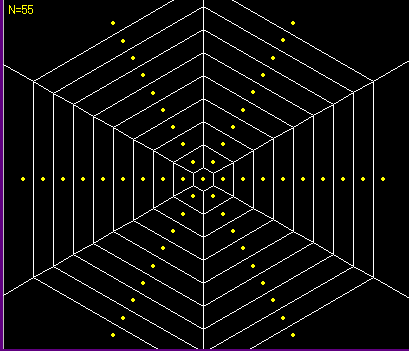Voronoi diagram like spider web 2

Voronoi diagram like beehive

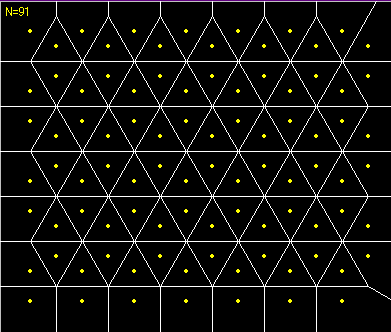Voronoi diagram for hexagonal lattice generators

Reference
A.Okabe, B.Boots, K.Sugihara, WILEY, SPATIAL TESSELLATIONS

Source of program

Java(voro.java 6KB)
MS Visual Basic(vbvoro.lzh)

Algorithm

i=1,...,N-1
    j=i+1,...,N
        Consider a bisector of p(i) and p(j)
        k=1,...,N except for i and j
            Consider a bisector of p(i) and p(k)
            Calculate the points of intersection of bisector(i,j) and bisector(i,k)
        next k
        Add the points x=0 and x=(the width of screen) of the bisector (i,j) into the points of intersections
        Sort the points of intersections in terms of x coordinates
        k=1,...,the number of intervals of the points of intersections
            Let c be a midpoint of the interval of the points of intersection.
            Let d be d(c,p(i))
            h=1,...,N except for i and j
                Let d' be d(c,p(h))
                If d'<d then shout (Out!)
            next h
            If we did not shout, then draw the interval of the points of intersection
         next k
    next j
next i

If you have a message, don't hesitate to send it by using
E-mail:

Mail Form
or
BBS

Use of Takashi Ohyama's website
English Home of Takashi Ohyama
Japanese Home of Takashi Ohyama